How Do Know When You Add or Subtractans Multiply and Divide Fractions
Introduction – Multiplying & Dividing Fractions
Tough creatures – The Fractions!
Fractions are considered to be one of the trickiest math concepts for young kids because it has dissimilar notations than whole numbers. It is an abstract notion that challenges the lilliputian rockstars to do amend.
Operations on fractions add together to the complication as it becomes strenuous for children to understand what these operations mean in physical and therefore, they visualize them for better understanding. The multiplication and division of fractions might be contradictory to the already existing understanding of multiplying and dividing whole numbers.
For example, multiplying two whole numbers always results in a greater production, but this is not the case with multiplying fractions
Similarly, dividing two whole numbers usually results in a caliber that is smaller than the dividend, but this is not the example with the dividing fractions.
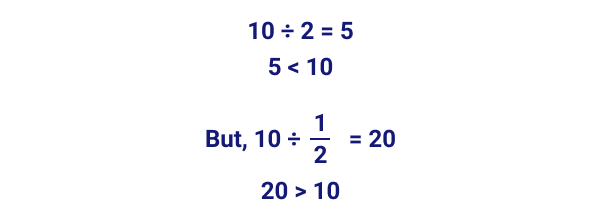
Due to the lack of deep understanding of these concepts, even among teachers, students take a hard time understanding fractions. Information technology as well paves way for defoliation and misconceptions among them.
The aim of this commodity is to provide engaging methods that would help children visualize multiplication and division concepts. Furthermore, we will besides try to ease the understanding of procedures involved in multiplying and dividing fractions through a unproblematic methodology involving only 4 steps.
Read on and brand learning fractions easy and pleasant!
Table of Contents
- Glossary
- Must-Knows
- Introduction to Multiplying Fractions
- First Step to Multiplying Fractions: Visual Modelling
- Multiplying Fractions: 4 Like shooting fish in a barrel Steps
- Analysis: Multiplying FractionsVersus Whole Number Multiplication
- Introduction: Dividing Fractions
- Showtime Footstep to Dividing Fractions: Visual Modelling
- Dividing Fractions: 4 Easy Steps
- Summary
- Frequently Asked Questions (FAQs)
Glossary
- Fraction – Part of a whole number written in the class of – a/b
- Denominator – The bottom number on a fraction
- Numerator – The number on the top of a fraction
- Unit Fraction – A fraction with numerator ane
- Whole Number – Counting numbers (0, i, two, iii, 4…)
- Equivalent fraction – A fraction that has equal/same value as some other fraction
- Simplifying – Making a fraction more elementary
- Proper fraction – A fraction with a value less than one (numerator < denominator)
- Improper fraction – A fraction with a value greater than 1 (numerator > denominator)
- Mixed Number – A way of writing improper fractions using a whole number and a proper fraction
- Divisor – A number by which another number is to be divided
- Dividend – A number that is to exist divided
- Quotient – The event of dividing one number past some other
- Rest – The leftover after division
Starting with the Multiplication & Division of Fractions: Must-Knows
- Understanding of multiplication and sectionalisation with whole numbers
- Agreement of fractions and their visual models
- Representing whole numbers as fractions
- Equivalent fractions
- Simplifying fractions to their lowest form
- Conversion of improper fraction into mixed number course and vice-versa
- Add-on of fractions
Introduction: Multiplying Fractions
Before starting with the steps of multiplying fractions, it is imperative to develop a conceptual understanding of fraction multiplication. Children should be able to visualize multiplication and should know what it means to multiply a fraction by a whole number or a fraction.
Quick Tip: It is suggested to start with modeling multiplication or sectionalization involving but whole numbers. You tin can and then move on to partial numbers. This way kids' existing cognition of multiplying or dividing whole numbers volition exist refreshed and they would be able to connect it to constructing the models for fraction multiplication or division.
Permit'southward start with Fraction Multiplication.
Kickoff Step to Multiplying Fractions: Modelling
Using visual models equally a learning assist makes the process of both pedagogy and learning more constructive, fun, and interactive. It is a educatee-centered arroyo and helps kids in visualizing fundamental mathematical concepts, which farther helps them to gain a deep conceptual understanding at a root level.
For the teachers, visual models can trigger discussions of mathematical ideas and relations with previously known concepts. It helps them accept a meliorate understanding of students' thought processes about the concept.
For that reason, teaching fraction multiplication initially through models and then proceeding towards standard procedures should exist the ideal arroyo.
To brainstorm with, Fraction Multiplication can take up 3 different forms.
Level 1A: Whole × Fraction
Level 1B: Fraction × Whole
Level 2: Fraction × Fraction
Delight note: We will not be taking upwardly mixed numbers as a divide case because these are also fractions written in a dissimilar course. To help your kids learn about mixed numbers and improper fractions through fun games, you lot can sign upwardly here!
Level 1A: Whole × Fraction
Example 1: Tim used ¼ of the pumpkin to make 1 pumpkin pie.
She made 3 pies. Let's discover out how many pumpkins she used in total.
As she used one-fourth of the pumpkin 3 times, its multiplication expression would be 3 × ¼
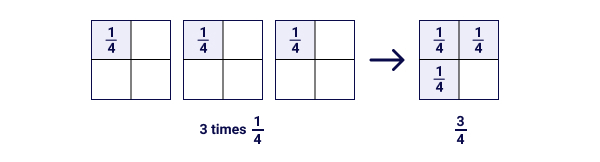
So,
3 × ¼ = iii/4
So, Tim used three-fourth of the pumpkin to brand three pies.
Example 2: If Tim had to brand 5 pies, how many pumpkins would she demand?
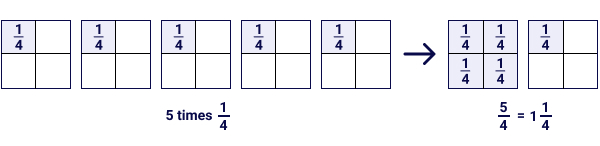
5 × ¼ = 5/4
So, Tim would need 1 whole and a quarter slice of the pumpkin to brand 5 pies.
Level 1B: Fraction × Whole
Visualizing the model for Fraction × Whole could be really challenging for the kids.
To get-go with, the offset number in the multiplication sentence denotes the number of groups or the number of times something is to be repeated. Simply, in the Fraction × Whole scenario, how do we class groups in a fractional number?
Example: ¼ × 8
We can describe this expression in elementary words as 1-fourth of eight . Mathematically, the word 'of' ways multiplication.
Let's depict a model for this expression.
Step 1:
Pace 2:
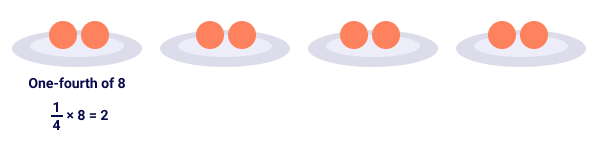
So, ¼ × 8 = two
Instance 1: ¾ × 8
This means: iii-fourth of eight
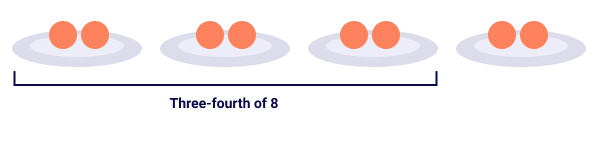
Then, ¾ × 8 = half-dozen
Allow'due south endeavor a few more examples.
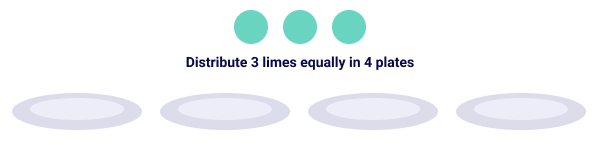
Case 2: Jamie prepared iv spectacles of juice using three limes. Find the number of lime fruits he used for each glass of juice.
This means he used a quarter of 3 limes to prepare one drinking glass of juice.
Mathematical Expression to be solved for this example: ¼ × iii
Permit's consider the three limes to be – A, B & C
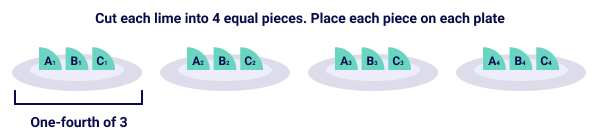
Each plate represents one-fourth or quarter of the whole lot, that is, 3 limes.
How many fourths are there in one plate? Three-fourths
So, ¼ × three = ¾
Jamie used ¾ of lime in one glass of juice.
Example 3: Find out how many limes did Jamie use for 3 glasses of juice.
This means that we need to find how much is three-fourth of 3 limes.
Mathematical Expression to be solved for this situation: ¾ × three
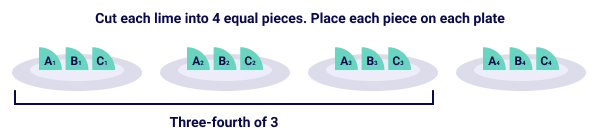
Each plate represents ane-fourth or quarter of the whole lot i.e 3 limes. So, three plates will represent three-fourths.
How many fourths are there in 3 plates? Ix-fourths

Then, ¾ × 3 = 9/iv
Jamie used nine/4 limes in three glasses of juice.

Level ii: Fraction × Fraction
Multiplying Fraction with Fraction is also a tricky form and students find it quite difficult to understand the application of multiplying two fractions.
Nosotros tin now help them visualize this concept through this engaging and uncomplicated paper folding activity.
Example 1: Visualise and Solve: ⅓ × ½
In general, this expression would mean 1-third of the half . You can help your child model this scenario using a sheet of newspaper.
Inquire your little learner to follow these simple steps:
- Take a rectangular sheet of newspaper and fold it into one-half.
- Next, fold the half into 3 equal parts.
- Color one of the folded sides, to show one-tertiary of the half.
- Open up the sail
- Identify what fraction of the whole does the shaded part represent
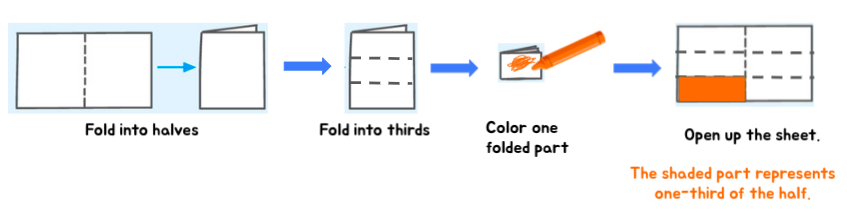
⅓ × ½ = ⅙
MUST TRY MORE!
Encourage your children to attempt multiplying different fractions using the aforementioned technique. Permit's explore a few more examples:
The following models follow the same principle as in the paper folding activity above. The principle mentioned is modeling two fractions in ane model.
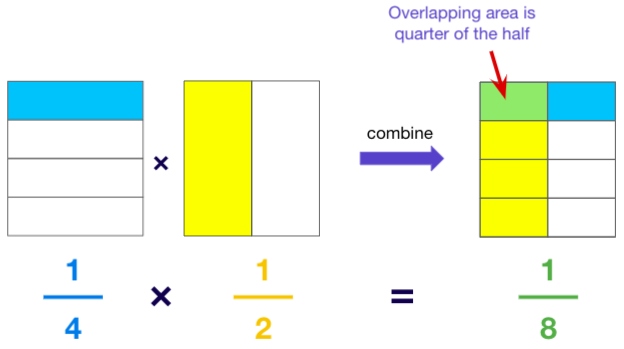
Instance ii: How much is ¼ × ½
This represents a quarter of one-half.

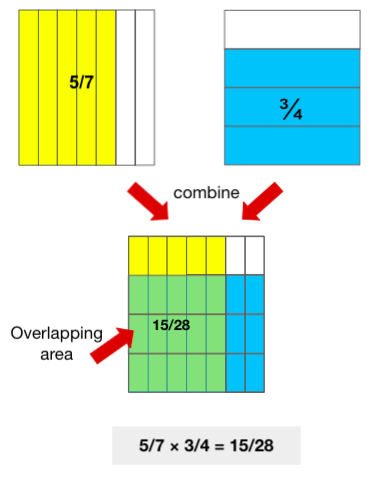
Example three: five/vii × ¾
Example iv: one/3 × i⅗
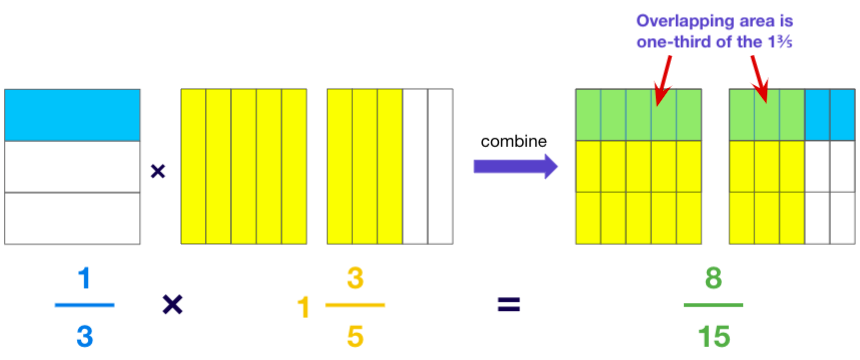
After a few examples, you tin encourage your child to direct draw the combined model.
Depict the model to multiply two fractions with these steps:
- Describe a big rectangle.
- Separate information technology into as many equal horizontal strips every bit the denominator of the kickoff fraction. Shade parts to represent the starting time fraction.
- Adjacent, split the same model into as many equal vertical strips as the denominator of the second fraction. Shade parts to represent the second fraction.
- Identify the overlapping part in the model. The fraction information technology represents is the production of the two fractions.
Multiplying Fractions: 4 Piece of cake Steps
Encourage the kids to find the products derived from the models along with telling what rule is existence followed in the multiplication of fractions.
Nosotros can help them empathize the process through these four easy steps of multiplying fractions.
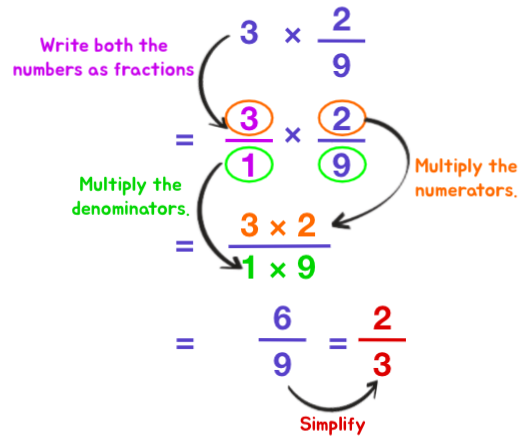
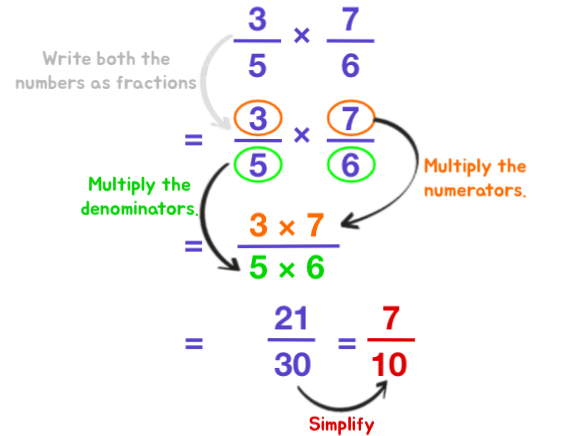
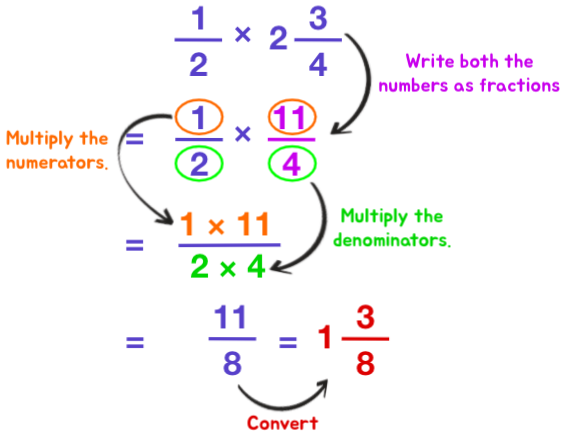
- Write both the numbers in fraction form.
- Multiply the numerators. The product is the new numerator.
- Multiply the denominators. The product is the new denominator.
- Rewrite the answer in the everyman or mixed number course.
Cheque out a few examples.
Example i:
Case ii:
Example 3:
Analysis: Multiplying Fractions versus Whole Number Multiplication
Question: Practise we always get a greater product on multiplying 2 numbers?
Notice the post-obit multiplication problems.
6 × 4 = 24
2 × 9 = 18
3 × 1 = 3
5 × vii = 35
10 × 8 = 80
19 × 1 = 19
8 × 0 = 0
7 × 11 = 77
16 × 2 = 32
Do you remember the same question holds for multiplication with fractions also?
The reply to that is 'sometimes'.
Let'south check out a few cases to understand those employ cases in a better capacity.
Instance i: When one of the multiplicands is 0
The production volition too exist a cypher regardless of what the other fraction is.
¼ × 0 = 0/4 = 0
⅗ × 0 = 0/v = 0
7/2 × 0 = 0/two = 0
Case 2: When one of the multiplicands is a fraction less than one
The product volition be smaller than the other fraction.
3/4 × 7/3 = 21/12 = seven/4 (< 7/3)
1/4 × 7/8 = 7/32 (< seven/8)
3/4 × one/9 = one/12 (< ane/nine)
Instance three: When one of the multiplicands is a fraction equivalent to 1
The production will be the same as the other number.
one × 7/8 = 7/8
6/6 × ix/5= 54/30= 9/5
6/6 × 3/5= eighteen/30= three/5
Instance 4: When one of the multiplicands is a fraction greater than 1
The product is will be greater than the other fraction
8/3 × 2/v= sixteen/15 (> 2/5)
half dozen/10 × nine/five= 54/50= 27/25 (> 6/10)
9/6 × i/7= 9/42= 3/14 (> 1/7)
Example 5: When both of the multiplicands are fractions greater than ane
The product will exist greater than both the fractions.
8/3 × 3/2 = four (> 8/3, iii/2)
6/iv × 5/two= 30/8 (> 6/4, five/2)
Dividing Fractions in Real Life: Introduction
We come up beyond situations in our day-to-twenty-four hours lives where we utilise the concept of fraction partition. Fraction partitioning can be fabricated interesting and the concept can be fully instilled in our kids' minds if they are challenged to solve scenarios from real life.
This would help the kids to visualize and make sense of fraction division.
Example: Suppose you have 3 apples, each cutting in one-half. To how many people can you distribute these iii apples, if each gets half a piece?
Let'due south picture this situation & solve it. Besides, an apple a day will definitely keep the math blues away!
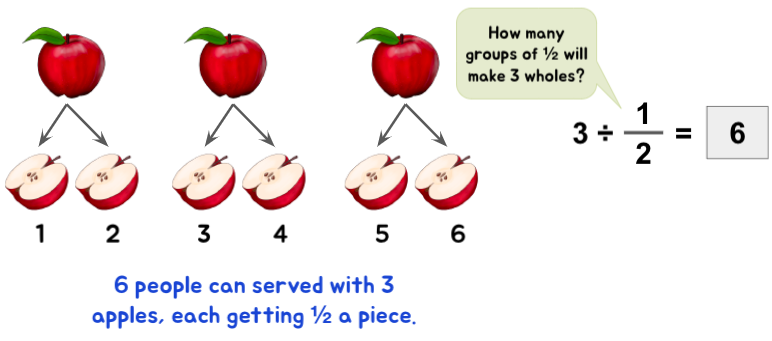
The problem tin can exist further extended by modifying the fraction.
For example, what if you determine to give each person a quarter slice? How many people tin be served now?
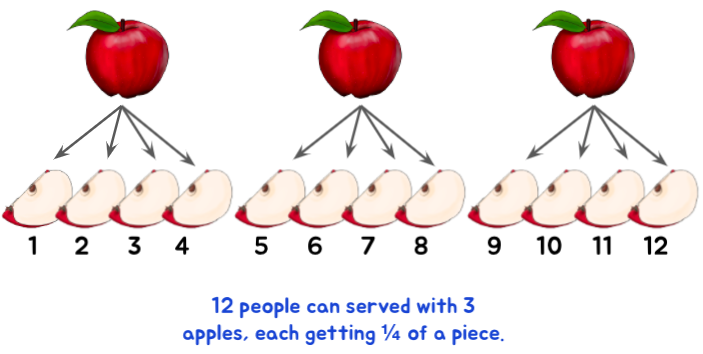
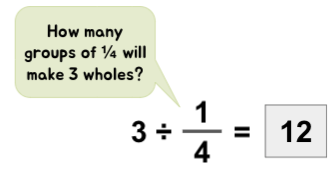
Or what if you decide to give each person three quarters? How many people can be served now?
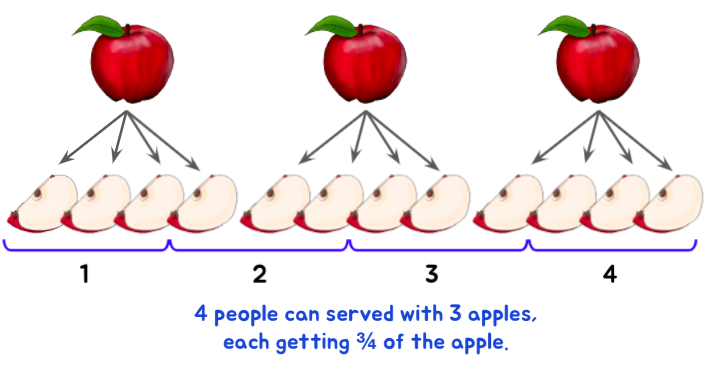
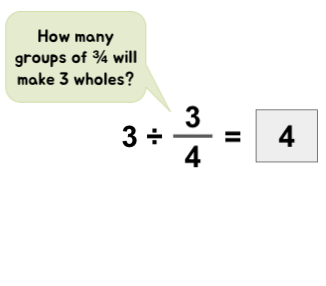
Comprehending a problem and then modeling information technology is a crucial footstep in whatsoever problem-solving scenario of fraction sectionalization. Encourage students to try visualizing the scenario then expect for its solution.
Draw and Solve!

A grouping of friends bought a pizza. They shared the pizza equally and finished it.
Effort identifying how many friends were there if each of them got—
| i-eighth of the pizza | two-8th of the pizza | |
| | | |
| eight friends | 4 friends | |
| And then, ane ÷ ⅛ = 8 | Then, 1 ÷ two/8 = 4 |
First Footstep to Dividing Fractions: Modelling
But like multiplication, once students gain expertise in modeling division problems for fractions, then the procedural method to find the answer is a breeze.
Therefore, for the partitioning of fractions likewise, information technology'southward suggested to use the approach from visual to non-visual method. For students, such an approach is more plausible as it lays a strong conceptual foundation.
Permit's come across a few examples.
Whole Number ÷ Fraction
Example i:
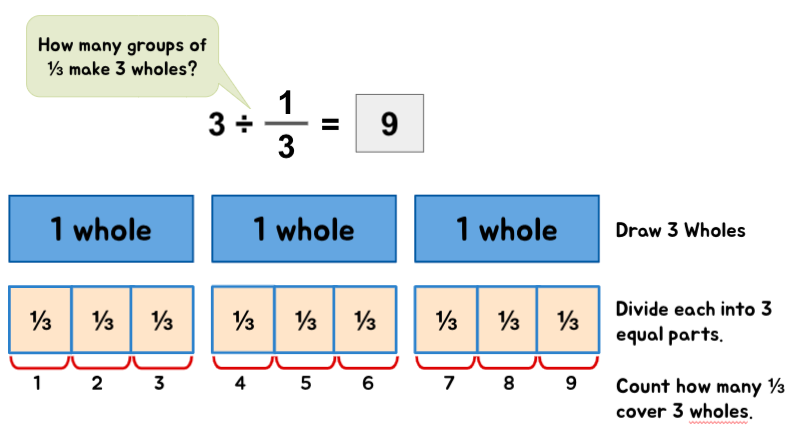
Example 2:
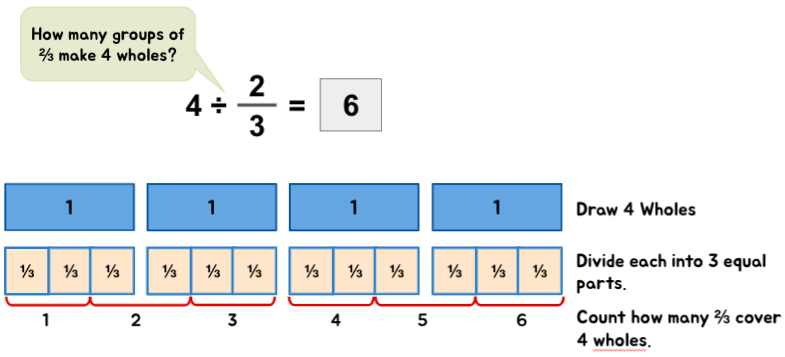
Quick Tip: When a divisor is a fractional number – information technology helps to depict the division statements as 'How many groups of (divisor) tin can exist formed from the (dividend)?' or 'How many groups of the (divisor) are there in the (dividend)'. These descriptions assistance children to visualize the situation at mitt with more ease.
Fraction ÷ Whole
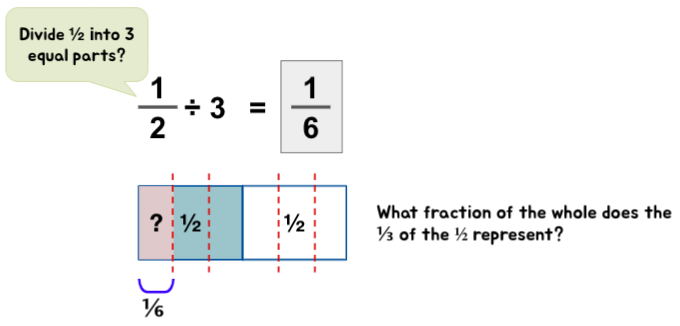
Fraction ÷ Fraction
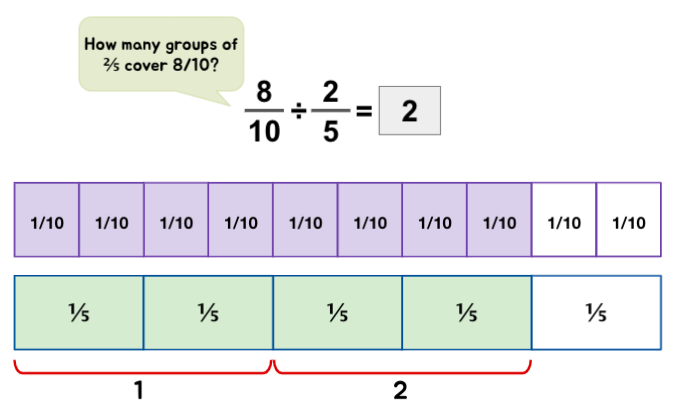
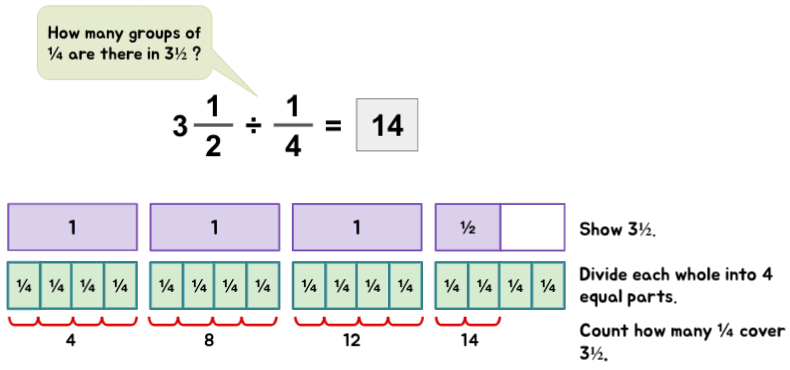
Mixed Number ÷ Fraction
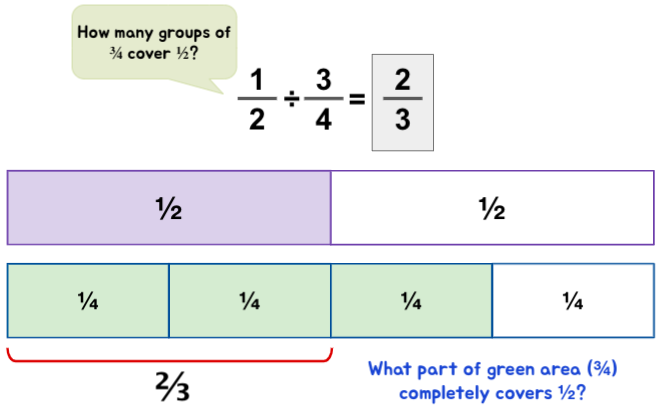
Dividing Fractions that Involve Remainder
Case 1
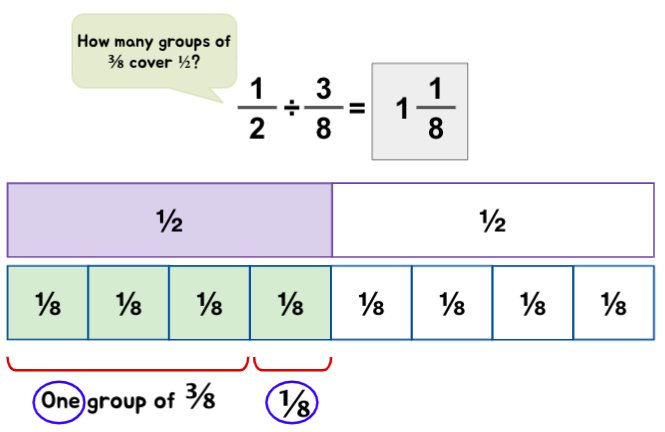
Example ii:
Some Common Struggles in Dividing Fractions
- Students oftentimes struggle to understand the difference between dividing by 2 and dividing past ½
Post-obit models can help them easily visualize the difference.
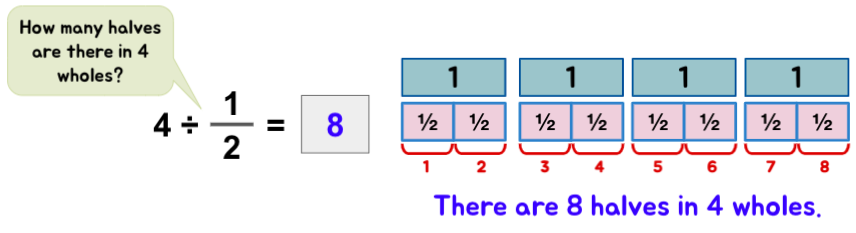
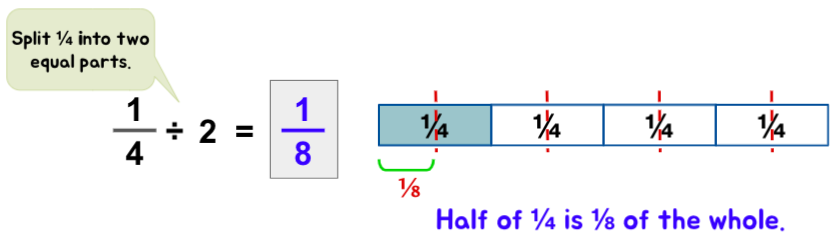
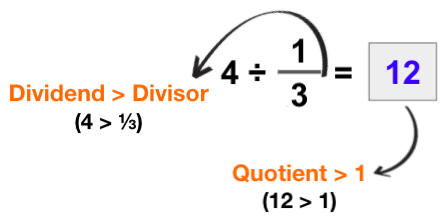
- Students often struggle to understand that information technology is non necessary that partition of fractions will e'er event in a smaller caliber.

Dividing Fractions: four Like shooting fish in a barrel Steps
It's imperative that nosotros encourage the children to observe the quotients derived from the models and tell what rule is beingness followed in the multiplication of fractions. Such activities with them help in developing inference and reasoning skills.
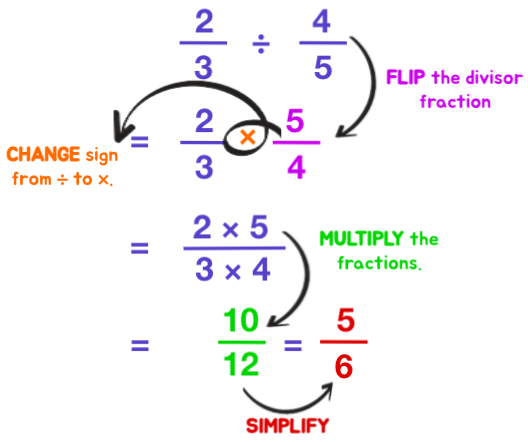
Aid them memorize the procedure through these 4 easy steps to divide fractions.
- Flip the divisor fraction
- Change sign from ÷ to ×
- Multiply the fractions
- Simplify
Key to Excel— Practice More than
Understanding fractions and their operations become a lot easier once children gain expertise in visualizing the problem and know what needs to be calculated. Only to gain such confidence, they need to practise a lot of issues. It'south necessary that they model the problem and so solve them.
You tin can refer to these worksheets on SplashLearn which are easily downloadable and printable, to assistance solidify your kid's understanding of multiplying fractions.
To sum up,
- For deeper understanding of the concept, brand certain to provide kids with the environment for experiential learning.
- Y'all tin employ your kids' previous and existing cognition of multiplying and dividing whole numbers to build the new knowledge of multiplying and dividing fractions.
- Encourage your kids to visualise problems and model them. Brand them experience comfy with asking questions.
- It's imperative to focus less on answering accurately and more on reasoning and thought procedure of the kid
- As a parent, relate the mathematical problems with existent life situations and provide instances from twenty-four hour period-to-day activities.
Make Fractions Easy with SplashLearn
With interactive games and rewards to heave your child'southward conviction and scores, y'all tin can now make learning piece of cake and seamless. Bring together our community of 40+ million fearless learners today!
Frequently Asked Questions (FAQs)
Q1 – How to multiply fractions footstep by stride?
- Write both the numbers in fraction form.
- Multiply the numerators.
- Multiply the denominators.
- Simplify or rewrite the reply in mixed number form.
Q2 – How to divide fractions step by stride?
- Flip the divisor fraction.
- Modify sign from ÷ to ×.
- Multiply the fractions.
- Simplify.
Q3 – How do you identify if multiplication by a fraction will result in a greater or a smaller product?
Compare the numerator and denominator of the fraction to check whether the production will be greater or smaller than the number to which they are multiplied.
Greater Product → Numerator > Denominator. Examples: 3/2, four/3, eight/5, and then on.
Smaller Product → Numerator < Denominator. Examples: 3/4, 4/7, 5/ix, and and so on.
Source: https://www.splashlearn.com/blog/how-to-multiply-divide-fractions-steps-with-visual-models/
0 Response to "How Do Know When You Add or Subtractans Multiply and Divide Fractions"
Post a Comment